Математика — наука интересная и увлекательная, в ней много софизмов и парадоксов.
В статье рассказываем, что такое курьезы, софизмы и парадоксы в математике, и какие парадоксы в этой науке существуют.
Еще больше полезных материалов из мира образования ищите на нашем Telegram-канале. И не забывайте следить за акциями и скидками от компании — с ними еще выгоднее учиться на отлично.
История возникновения парадоксов в математике
Принято считать, что математика — это точная наука, которая не терпит погрешностей. На самом деле, математика полна противоречий и неточностей. В этой науке есть такие понятия, как парадоксы и софизмы.
Математические парадоксы — это явления, которые могут быть на самом деле, но относительно них нет логических объяснений.
Главная особенность парадоксов состоит в том, что определенное утверждение может быть и верным, и ложным одновременно.
А вот софизм — это утверждение, которое кажется верным на первый взгляд, однако, при детальном рассмотрении, оно будет ошибочным.
В софизмах ошибка может быть допущена как случайно, так и умышленно.
Главная составляющая таких математических уловок — нарушение логики. В математике, чтобы прийти к какому-то заключению, надо сначала хорошенько поразмышлять. Длительные логические рассуждения часто и провоцируют разного рода ошибки.
Интересные парадоксы в математике: примеры
Парадоксов в математике очень много. Мы собрали для вас самые занимательные и необычные.
Парадокс орнамента
Многие в детстве любили наблюдать за узорами на коврах или обоях, они казались такими красивыми и бесконечными. На самом деле, бесконечность орнамента — это заблуждение, или математический парадокс.
Если углубиться в архитектуру, то можно выяснить, что есть всего 17 групп орнаментов. Это означает, что узоры не бесконечны, и даже если один орнамент сменяет другой, они все равно когда-то закончатся.
Если говорить языком математики, то количество фигур на обоях — ограничено. Причем неважно, какого цвета, формы и размера орнамент — все равно он входит в одну из семнадцати архитектурных групп, и в итоге будет иметь конец.
Парадокс кучи
Все в этом мире относительно: что для одного человека может быть небольшим, для другого окажется значительным.
Как понять, когда маленькое зернышко может стать кучей зерен? Как определить, что такое куча и когда она начинается? Об этом давным-давно задумался древнегреческий ученый Евбулид. Он назвал этот феномен парадоксом сорита. Парадокс кучи гласит, что если к зернышку добавлять по одному зерну, то это количество зерна не будет становиться кучей, и никакое количество зерна не будет образовывать кучу. Это объясняется тем, что добавление зерна к совокупности, которая кучей не является, совсем несущественно для образования кучи.
На основании этого парадокса мыслитель сформулировал и другие софизмы. Например, если у человека начнут по одному выпадать волосы, когда он станет лысым, или сколько волос должно остаться на голове у человека, чтобы его стали называть лысым?
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы.

Парадокс картофеля
Парадокс картофеля в математике — известное заблуждение, которое базируется на интуиции, вернее, на ее обманчивости.
Суть этого парадокса в следующем: например, у человека есть 100 кг картофеля, масса воды в овоще — 99%. Допустим, картофель решили высушить до 98% воды. Вопрос: сколько теперь весят овощи? Логика нам подсказывает, что останется 2 кг., но это говорит не логика, а интуиция.
Если подумать логически, то при высушивании картошки на 98%, сухого вещества там останется 2% от общей массы. Если говорить математическим языком, то это будет соотношение 2 к 98, которое можно сократить как 1 к 49. Сухое вещество не изменилось, оно осталось весить 1 кг, значит, вода будет весить 49 кг. Если сложить эти величины, то получится 50 кг. Неожиданный ответ, правда?
Этот парадокс в математике еще часто называют парадокс кукурузы, парадокс капусты, тыквы и т.д.Этот парадокс овощей в математике свидетельствует, что интуиция и первое суждение часто бывает ошибочным.
Парадокс маляра
Существует парадокс маляра. Парадокс маляра в математике гласит о том, что фигуру с бесконечной площадью поверхности можно окрасить определенным количеством краски. Как так может быть? Давайте разберемся.
Представьте, что вы красите фигуру, например, прямоугольник. Вы покрасили сантиметр, два, три, десять... С каждым разом и каждым слоем краски на каждый элемент потребуется все меньше и меньше. Если подойти к задаче логически и со стороны маляра, то фигуру надо красить равномерным слоем краски. Тогда с каждым слоем окрашивания краски будет надо все меньше.
В итоге количество краски будет уменьшаться и станет определенным числом, а не бесконечным.
Парадокс дней рождения
Есть еще один парадокс в математике — дней рождения.
Представим, что есть группа людей из 23 человек. Оказывается, что в этой группе число и месяц рождения могут совпасть у двух человек как минимум в 50% случаев. А вот если людей в группе добавится и станет, например, 60, то вероятность совпадения возрастет до 99%. А стопроцентная вероятность совпадения станет, если в группе станет не меньше 366 человек. Как такое возможно, ведь эти рассуждения совсем противоречат логике? Или опять нас обманула наша интуиция?
Предположим, что в группе первокурсников из 23 человек у студента А день рождения — 1 сентября. Вероятность того, что и у студента Б именины будут в этот день — 1 к 365 (365 — это количество дней в году). Если записать математически, то получится такое выражение:
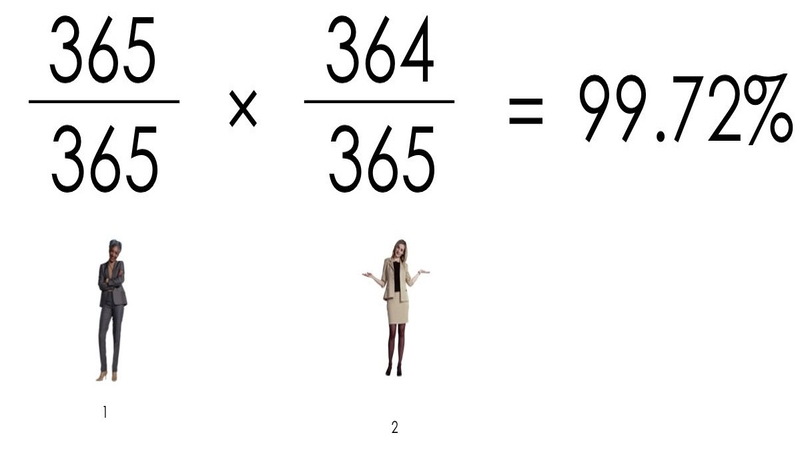
Если в группе 23 человека, то округленное число совпадений — 1/2, а это 50%, что и требовалось доказать.
Вот такие математические парадоксы бывают. Согласитесь, некоторые из них идут вразрез с логикой и взрывают мозг. Справиться с этими и другими учебными задачами вам, как всегда, помогут специалисты студенческого сервиса.