В нашей отдельной статье можно почитать про работу и энергию в классической механике. А сегодня займемся решением задач на закон сохранения энергии.
Вот здесь у нас есть полезная памятка по решению физических задач. А на нашем телеграм-канале вас ждет ежедневная рассылка с интересной информацией для студентов абсолютно всех специальностей.
Закон сохранения энергии
Сначала о том, почему этот закон (или, вернее сказать, принцип) называют фундаментальным?
Этот закон определяет закономерность, справедливую всегда и везде, не относящуюся к конкретным величинам и явлениям. Принцип сохранения справедлив для всей Вселенной.Закон сохранения энергии - установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени.
В разных областях физики закон сохранения был независимо выведен в разное время. Формулировки для разных видов энергии также отличаются. Для термодинамики это первое начало, а для классической механики – закон сохранения механической энергии.
Сегодня мы будем рассматривать решение задач как раз на тему сохранения механической энергии. Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Примеры решения задач
Задача 1
Максимальная высота, на которую поднимается тело массой 1 кг, подброшенное вертикально вверх, составляет 20 м. Найдите, чему была равна кинетическая энергия сразу же после броска.
Решение
Эта задача простая и не требует рисунка. Потенциальная энергия тела над поверхностью Земли вычисляется по формуле:
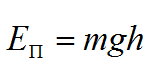
Здесь m – масса тела, g – ускорение свободного падения, h – высота. Согласно закону сохранения энергии, потенциальная энергия тела в наивысшей точке должна равняться кинетической энергии тела в начальный момент, то есть

Принимая ускорение свободного падения равным 10 м/с2, находим кинетическую энергию тела сразу же после броска:

Ответ: 200 Дж.
А вот пример задачи по физике с ЕГЭ
Задача 2
Шарик висит на нити. В нем застревает пуля, летящая горизонтально, в результате чего нить отклоняется на некоторый угол. Как изменятся при увеличении массы шарика следующие величины: импульс, полученный шариком в результате попадания в него пули; скорость, которая будет у шарика тотчас после удара; угол отклонения нити? Пуля застревает очень быстро. Для каждой величины определите соответствующий характер изменения.
Решение
Согласно закону сохранения импульса, скорость шарика с застрявшей в нем пулей равна

где M и m – массы шарика и пули соответственно, v – скорость пули перед ударом. Таким образом, при увеличении массы шарика его скорость после удара уменьшится. Найдем импульс, переданный шарику при попадании пули:
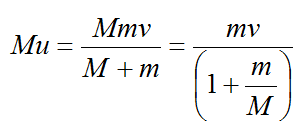
Следовательно, с увеличением массы шарика переданный ему импульс увеличивается. Согласно закону сохранения энергии, кинетическая энергия пули перейдет в потенциальную энергию шарика с пулей:
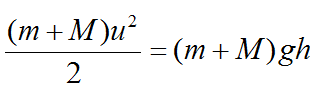
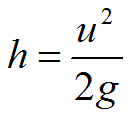
Таким образом, при увеличении массы шарика угол отклонения нити уменьшится, поскольку уменьшится скорость u.
И третья задача на вращательное движение.
Задача 3
На горизонтальную цилиндрическую ось массой m1 и радиусом R1 насажен маховик массой m2 и радиусом R2. На маховик намотана нить, к которой прикреплен груз массой М. Груз начинает двигаться под действием силы тяжести и через некоторое время t опускается на расстояние H. Движение груза равноускоренное. Записать закон сохранения энергии для груза и маховика. Записать кинетическую энергию вращения маховика, кинетическую и потенциальную энергию груза, как функции времени t.
Решение
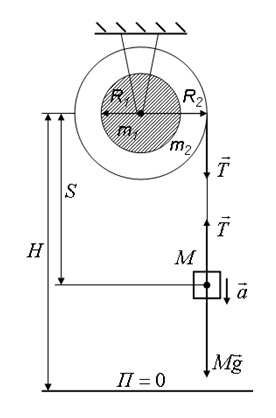
Закон сохранения энергии для груза и маховика:
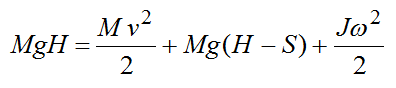
Слева – потенциальная энергия груза в начальный момент времени. Справа – кинетическая энергия груза, потенциальная энергия груза, кинетическая энергия вращения маховика. За начало отсчета потенциальной энергии груза принимаем его конечное положение.
Кинетическая энергия груза:

Потенциальная энергия груза:
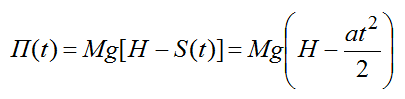
Кинетическая энергия вращения маховика:

Нужна помощь в решении задач? Обращайтесь в профессиональный студенческий сервис.











