Задачи на тему «Тонкие линзы» с решением

Задачи по геометрической оптике не такие уж и сложные, если уделить их разбору немного временени. Сегодня в нашей регулярной рубрике «Физика для чайников» рассмотрим несколько примеров задач на тонкие линзы.

Хотите быть в курсе актуальных новостей, связанных с учебой? Присоединяйтесь к нам в телеграме! А тем, кто хочет получать скидки и бонусы, рекомендуем заглянуть на наш второй канал для клиентов.

Тонкая линза: задачи

Чтобы успешно решать задачи по геометрической оптике на тему «Тонкие линзы», нужно знать всего лишь пару формулу. Правда, формул много не бывает, и мы собрали их вместе: пригодятся в решении задач по другим темам. А тем, кто не знает, как вообще подступиться к задачам по физике, рекомендуем почитать общую памятку по решению. 

Задача №1. Формула тонкой линзы

Условие 

Линзу с оптической силой 2,5 дптр поместили на расстоянии 0,5 м от ярко освещённого предмета. На каком расстоянии следует поместить экран, чтобы увидеть на нём чёткое изображение предмета?

Решение

Линза является собирающей (оптическая сила положительна). Запишем формулу тонкой линзы:

$\frac{1}{F}=\frac{1}{d}+\frac{1}{f}$

Учтем, что $F=\frac{1}{D}$, подставим значения из условия, и запишем:

$$\begin{gathered} 2,5=\frac{1}{0,5}+\frac{1}{+f} \\ f=2 м \end{gathered}$$

Ответ: 2м

Задача №2. Формула тонкой линзы

Условие

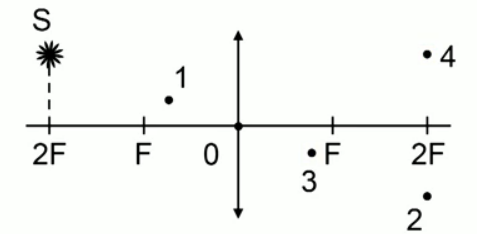
Светящаяся точка лежит в плоскости, проходящей через двойной фокус тонкой линзы, у которой указана главная оптическая ось. Определите, какая из четырех точек на чертеже соответствует правильному изображению  светящейся точки.

Решение

Как видим, на рисунке изображена собирающая линза с оптическим центром в точке 0. Светящася точка S находится от линзы на расстоянии, равном двум фокусам.

Построим изображение точки: один луч проходит через оптический центр линзы, а второй луч, параллельный главной оптической оси, после преломления проходит через фокус. Точка пересечения лучей на расстоянии двойного фокуса и будет являться изображением точки S.

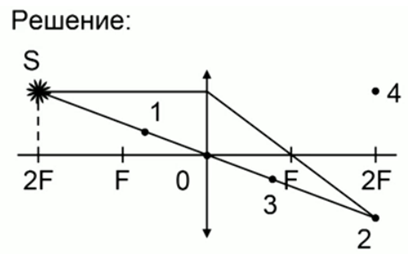
Ответ: изображению точки S соответствует точка 2.

Денное решение получено геометрическим путем, но его можно проверить, используя формулу линзы. Подставим в нее 2F вместо d, и получим тот же результат.

Задача №3. Формула тонкой линзы

Условие

Предмет высотой 3 см находится на расстоянии 40 см от собирающей тонкой линзы. Определите высоту изображения, если оптическая сила линзы равна 4 диоптриям.

Решение

Запишем форумулу тонкой собирающей линзы и формулу увеличения линзы:

$\frac{1}{F}=\frac{1}{d}+\frac{1}{f} ; Г=\frac{H}{h}=\frac{\left|f\right|}{\left|d\right|}$

Перепишем эти соотношения, с учетом того, что $F=\frac{1}{D}$

$$\begin{gathered} H=h·\frac{\left|f\right|}{\left|d\right|} \\ \frac{1}{f}=D-\frac{1}{d} \end{gathered}$$

Отсюда найдем f:

$f=\frac{d}{D·d-1}$

Осталось подставить значения в формулу для H и вычислить:

$H=\frac{hd}{D·d-1}=\frac{0,03·0,4}{4·0,4-1}=0,05 м$

Ответ: 0,05 м.

Задача №4. Формула тонкой линзы

Условие

Предмет имеет высоту 2 см. Какое фокусное расстояние должна иметь линза, расположенная на расстоянии f=4 м от экрана, чтобы изображение предмета на экране имело высоту H=1 м?

Решение

Фокусное расстояние найдем из формулы линзы:

$$\begin{gathered} \frac{1}{F}=\frac{1}{d}+\frac{1}{f} \\ F=\frac{fd}{d+f} \end{gathered}$$

Запишем формулу увеличения линзы и выразим d:

$Г=\frac{H}{h}=\frac{\left|f\right|}{\left|d\right|} ; d=\frac{fh}{H}$

Запишем окончательный ответ:

$F=\frac{hf}{H+h}\approx 0,08 м$

Ответ: 0,08 м.

Задача №5. Формула тонкой линзы

Условие

Постройте изображение отрезка AB, расположенного перед собирающей линзой так, что расстояние от предмета до линзы d=2F. Каким будет изображение?

Решение

Посторим изображение в соответствии с правилами геометрической оптики:

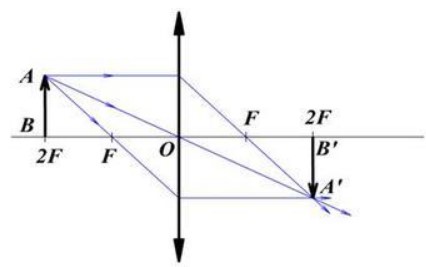
Данное изображение:

• действительное;
• перевернутое;
• равное предмету.

Ответ: см. выше.

Вопросы на тему «Тонкая линза»

Вопрос 1. Какое равенство называют формулой тонкой линзы?

Ответ. Формула тонкой линзы имеет следующий вид:

$\frac{1}{F}=\frac{1}{d}+\frac{1}{\pm f}$

Здесь:

• F – фокусное расстояние;
• d – расстояние от линзы до предмета;
• f – расстояние от линзы до изображения. 

Вопрос 2. В чем разница в формуле линзы для собирающей и рассеивающей линз?

Ответ. Для собирающей линзы f берется положительным, а для рассеивающей – отрицательным. Соответственно, собирающая линза строит действительное изображение, а рассеивающая – мнимое.

Вопрос 3. Что такое фокусное расстоняние линзы?

Ответ. Фокусное расстояние линзы – это расстояние между ее оптическим центром и главным фокусом.

Вопрос 4. Что такое оптическая сила линзы?

Ответ. Оптическая сила – это величина, обратная фокусному расстоянию. Она характеризует преломляющую способность линзы.

Вопрос 5. Может ли оптическая сила линзы быть отрицательной?

Ответ. Да. Для рассеивающей линзы оптическая сила берется со знаком минус.

Проблемы с решением задач или других заданий? Обращайтесь в профессиональный сервис помощи учащимся!