Никакой воды. Только типовые задачи с подробным разъяснением и ответом.
Полезная и ежедневная рассылка для студентов всех специальностей – на нашем телеграм-канале.
Задача 1
Три одинаковых точечных заряда q1=q2=q3=2 нКл находятся в вершинах равностороннего треугольника со стороной a=10 см. Определить модуль и направление силы F, действующей на один из зарядов со стороны двух других.
Решение
Очевидно, задача требует рисунка. Выполним его:
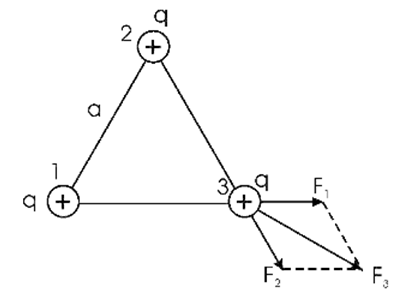
В данной задаче при решении применяется закон Кулона:
Сила взаимодействия двух точечных зарядов в вакууме направлена вдоль прямой, соединяющей эти заряды, пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними. Она является силой притяжения, если знаки зарядов разные, и силой отталкивания, если эти знаки одинаковы.
Сила, с которой взаимодействуют заряды 1 и 2 равна:
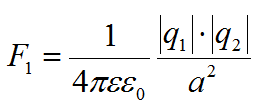
Так заряды равны, то
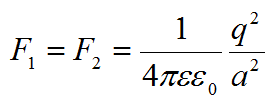
Треугольник равносторонний, все его углы равны 60 градусов. Искомая сила направлена по биссектрисе угла и находится по формуле:
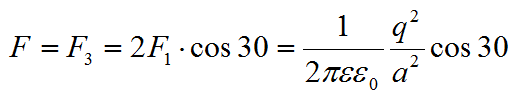
Осталось подставить значения из условия и вычислить:
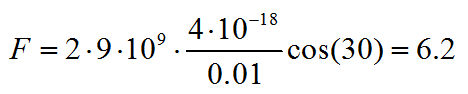
Ответ: 6,2 мкН.
Задача 2
Два положительных точечных заряда Q и 9Q закреплены на расстоянии d=100 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещение зарядов возможны только вдоль прямой, проходящей через закрепленные заряды.
Решение
Снова выполним рисунок:
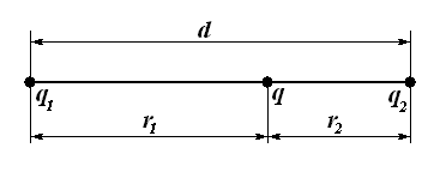
Для равновесия зарядов необходимо, чтобы они действовали друг на друга с одинаковыми силами:
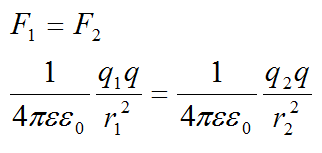
Из условия можно вычислить:

Сократим и перепишем равенство сил:
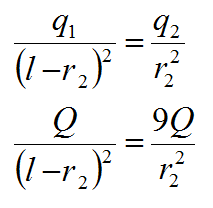
Отсюда находим:
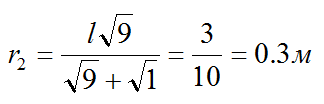
При вычислении не забываем переводить все величины в систему СИ
Для устойчивого равновесия заряд q должен быть положительным. Если он сместится из положения равновесия ближе к заряду q2, то сила отталкивания со стороны этого заряда возрастет, а со стороны заряда q1 – уменьшится, и заряд q возвратится в положение равновесия.
Ответ: r1=0.7м, r2=0.3м, заряд положительный.
А теперь задача посложнее, с интегралами. Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Задача 3
Тонкий стержень длиной l=10 см равномерно заряжен с линейной плотностью заряда τ=1 мкКл/м. На продолжении оси стержня на расстоянии d=20см от ближайшего его конца находится точечный заряд Q1 =100нКл. Определить силу взаимодействия заряженного стержня и точечного заряда.
Решение
Вот как выглядит рисунок к этой задаче:
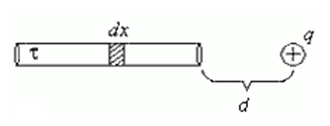
Закон Кулона позволяет вычислить силу взаимодействия точечных зарядов. По условию задачи, один из зарядов не является точечным, а представляет собой заряд, равномерно распределенный по длине стержня. Если выделить на стержне дифференциально малый участок длиной dx, то находящийся на нем заряд dQ=τ·dx можно рассматривать как точечный, и тогда по закону Кулона сила взаимодействия между зарядами Q1 и dQ.
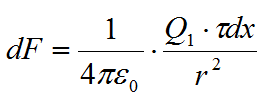
r — расстояние от выделенного элемента до заряда Q1. В условии задачи не указана среда это значит, что заряды находятся в вакууме (ε=1). Чтобы найти силу, проинтегрируем выражение:
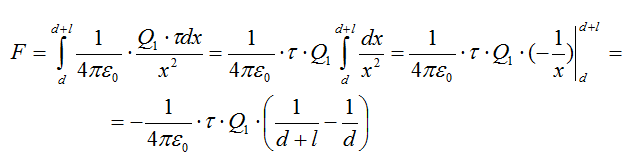
Подставляем значения и получаем:
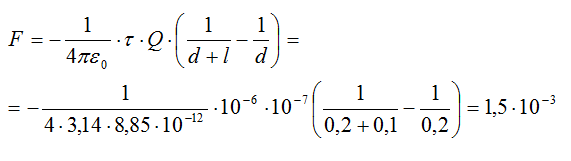
Ответ: 1,5∙10-3Н
За скорой помощью в решении задач разной сложности обращайтесь к специалистам студенческого сервиса.











