Задачи на интерференцию света с решением

В нашей традиционной рубрике «Физика для чайников» сегодня решение задач. Тема – интерференция света. Разберем несколько типовых задач и ответим на вопросы.

Хотите читать не только о скучных задачах, но и получать актуальные студенческие новости? Подпишитесь на наш телеграм! А за скидками на услуги и акциями для клиентов добро пожаловать на наш второй канал.

Интерференция света: решение задач

Чтобы решать задачи, сначала нужно изучить теорию. Также мы собрали вместе формулы, которые пригодятся для решения задач по интерференции света, и не только. А тем, кто еще не знает, как вообще подступиться к физическим задачам, рекомендуем почитать общую памятку. А теперь, примеры решения задач по интерференции.

Задача №1 на интерференцию света

Условие

Высота радиомаяка над уровнем моря H = 200 м, расстояние до корабля d = 5,5 км. Определить оптимальную высоту мачты корабля для приема сигналов с длиной волны равной 1,5 м.

Решение

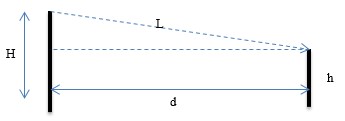
В данном случае волна, исходящая от радиомаяка, интерферирует с волной, отражённой от поверхности воды. Условие m-го максимума:

$y_m=\frac{\left(2m-1\right)d\lambda }{4H}$

Для нахождения оптимальной высоты мачты примем m=1:

$y=\frac{d\lambda }{4H}=\frac{5500·1,5}{4·200}=10,3м$

Ответ: 10,3 м.

Задача №2 на интерференцию света

Условие

Источник света S с длиной волны 400 нм создает в схеме Юнга два когерентных источника, помещенных в бензол (n = 1,5). В точку А на экране луч от первого источника дошел за t1 =2,0000*10-10 c, а от второго за t2 =2,0002*10-10 c. Определить разность фаз колебаний в точке А и порядок интерференции k.

Решение

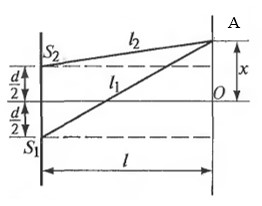
Найдем расстояния $l1$, пройденное лучом:

$$\begin{gathered} l1=v·t_1=\frac{c}{n}·t_1 \\ l1=\frac{3·{10}^8}{1,5}·2,0000·{10}^{-10}=4 см \end{gathered}$$

Найдем расстояние $l2$:

$$\begin{gathered} l2=v·t_2=\frac{c}{n}·t_2 \\ l2=\frac{3·{10}^8}{1.5}·2,0002·{10}^{-10}=4,0004 см \end{gathered}$$

Таким образом, разность хода составляет:

 $∆х=0,0004 см=4·{10}^{-6} м$

Найдем разность фаз:

$$\begin{gathered} ∆\phi =\frac{2\pi ∆х}{\lambda } \\ ∆\phi =\frac{2\mathrm{\pi }·4·{10}^{-6}}{4·{10}^{-7}}=62,8 \end{gathered}$$

Условие максимума для интерференции:

$$\begin{gathered} ∆\phi =\pm 2\mathrm{\pi k} \\ 2\mathrm{\pi k}=62,8 \end{gathered}$$

В данной точке порядок интерференции k=10.

Ответ: $∆\phi =62,8 ; k=10$.

Задача №3 на интерференцию света

Условие

Найти расстояние от точки 0 на экране P в установке бипризмы Френеля до m-ой светлой полосы, если показатель преломления бипризмы n = 1,5, длина волны 500 нм, преломляющий угол  альфа = 3 мин.26сек. (m = 6, а = 0,2 м, в = 1 м).

Решение

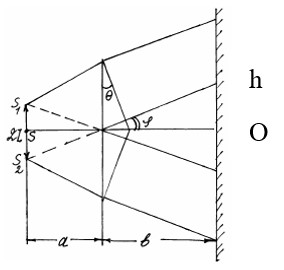
Условие максимума в данном случае:

$∆=m\lambda$

Из рисунка можно получить, что:

$h=\frac{\left(∆\left(a+b\right)\right)}{2l}=\frac{\left(m\lambda \left(a+b\right)\right)}{2l}$

где $2l$ – расстояние между источниками, m-порядковый номер максимума.

Из рисунка:

$2l=2a·\sin \phi =2a\phi$

Последнее предполоежение сделано вследстиве малости угла.

Тогда получаем:

$h=\frac{\left(m\lambda \left(a+b\right)\right)}{2a\phi }$

Связь между преломляющим углом бипризмы Θ и φ определяется известной формулой: 

$\left(n-1\right)\theta =\phi$

В итоге:

$h=\frac{\left(m\lambda \left(a+b\right)\right)}{\left(2a\left(n-1\right)\theta \right)}$

Подставляя численные значения получаем:

$h=\frac{6·5·{10}^{-7}·\left(0,2+1\right)}{2·0,2\left(1,5-1\right)·9,99·{10}^{-4}}=1,8·{10}^{-2} м$

Ответ: 1,8 см.

Задача №4 на интерференцию света

Условие

На стеклянный клин нормально к поверхности падает пучок света (λ = 582 нм). Угол клина равен 20". Какое число интерференционных полос приходится на единицу длины клина? Показатель преломления стекла равен 1,5.

Решение

Ширина интерференционных полос при интерференции на прозрачном клине равна:

$B=\frac{\lambda }{2n\alpha }=\frac{585·{10}^{-9}·3600·180}{2·1,5·20·3,14}=2·{10}^{-3} м$

Найдем число интерференционных полос, приходящихся на один сантиметр клина:

$N=\frac{{10}^{-2}}{2·{10}^{-3}}=5 с{м}^{-1}$

Ответ: 5 полос на сантиметр

Задача №5 на интерференцию света

Условие 

Найти радиус кривизны стеклянной плоско-выпуклой линзы, примененной для получения колец Ньютона, если радиус третьего светлого кольца равен 1,4 мм; длина волны 589 нм. Кольца наблюдаются в отраженном свете.

Решение

В отраженном монохроматическом свете радиусы светлых колец равны:

$r=\sqrt{\frac{\left(2m+1\right)R\lambda }{2}}$

Радиус кривизны линзы R найдем из этой формулы:

$R=\frac{4r^2}{\left(2m+1\right)\lambda }=\frac{4·{\left(1,4·{10}^{-3}\right)}^2}{\left(2·3+1\right)·589·{10}^{-9}}=1,9 м$
 

Ответ: 1,9 м. 

Нужно больше задач по оптике? У нас есть!

Вопросы на интерференцию света

Вопрос 1. Что такое интерференция?

Ответ. Интерференцией называется постоянное во времени явление взаимного ослабления и усиления колебаний в разных точках среды в следствии наложения когерентных волн.

Вопрос 2. Когда можно наблюдать интерференцию?

Ответ. Это явление наблюдается при наложении двух или нескольких световых пучков. Интенсивность света в области перекрытия пучков имеет характер чередующихся темных и светлых полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков.

Вопрос 3. Приведите примеры интерференции, с которыми мы часто сталкиваемся в жизни.

Ответ. Проявление интерференции света:

• цвета  масляных пятен и мыльных пузырей на асфальте;
• окраска замерзающих оконных стекол; 
• цветные рисунки на крыльях некоторых жуков и бабочек.

Вопрос 4. Что влияет на интенсивность света в конкретной точке интерференционной картины?

Ответ. Интенсивность света в данной точке пространства определяется разностью фаз колебаний световых волн.

Вопрос 5. Проявлением какой природы света является интерференция: волновой или корпускулярной?

Ответ. Интерференция – проявление исключительно волновой природы.

Проблемы с решением задач? Обращайтесь в профессиональный сервис помощи учащимся в любое время суток!