Теорема Гаусса выражает связь между потоком вектора напряженности электрического поля через замкнутую поверхность и алгебраической суммой зарядов, заключенных в объеме, ограниченном этой поверхностью. О примерах использования теоремы Гаусса на практике поговорим в этой статье.
Присоединяйтесь к нам в телеграме, чтобы не только решать задачи, но и быть в курсе актуальных новостей для студентов всех специальностей.
Задачи на теорему Гаусса с решением
Если вам нужно сначала освежить теоретические знания, читайте подробную теорию по теореме Гаусса в нашем справочнике. Ну а перед решением задач не забудьте повторить памятку и на всякий случай держите под рукой полезные формулы.
Кстати, при решении задач на теорему Гаусса придется довольно часто брать интегралы. Хотите научиться делать это по-быстрому? У нас уже есть отдельная статья и видео на эту тему.
Задача на теорему Гаусса №1: напряженность поля плоскости
Условие
Определите напряженность поля бесконечной заряженной плоскости. Поверхностная плотность заряда сигма.
Решение
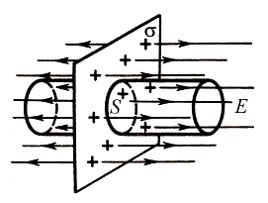
Линии напряженности перпендикулярны рассматриваемой плоскости и направлены в обе стороны от неё. Выберем в качестве гауссовой поверхности цилиндр с основанием, параллельным плоскости:
По теореме Гаусса:
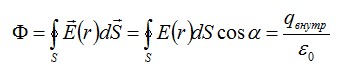
Поток сквозь цилиндр равен сумме потоков сквозь боковую поверхность цилиндра и потокам сквозь оба его основания. Поток сквозь боковую поверхность равен нулю, так как линии напряженности параллельны ей:
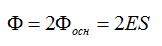
Согласно теореме Гаусса:
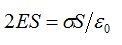
Отсюда:
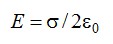
Ответ: см. выше.
Задача на теорему Гаусса №2: напряженность поля двух пластин
Условие
Электрическое поле создано двумя параллельными заряженными тонкими пластинами с поверхностными плотностями заряда + сигма и -2 сигма. Площадь каждой пластины S, расстояние между пластинами d можно считать значительно меньшим их продольных размеров. Какова напряженность электрического поля, созданного этими пластинами?
Решение
Для электрического поля действует принцип суперпозиции: результирующее поле равно векторной сумме отдельных полей каждой пластины. Из предыдущей задачи мы знаем формулу, по которой вычисляется напряженность поля тонкой заряженной пластины, запишем для каждой из них:
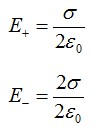
Векторы напряженности между пластинами совпадают по направлению, результирующая напряженность равна:
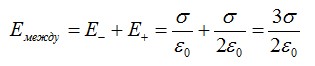
Справа и слева от пластин, во внешней области, векторы направлены в разные стороны:
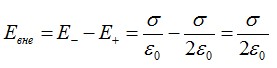
Для наглядности приведем рисунок:
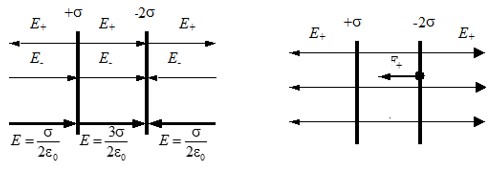
Ответ: см. выше.
Задача на теорему Гаусса №3: напряженность электрического поля бесконечной нити
Условие
Определить напряженность электрического поля, создаваемую бесконечной тонкой нитью, равномерно заряженной с линейной плотностью заряда лямбда.
Решение
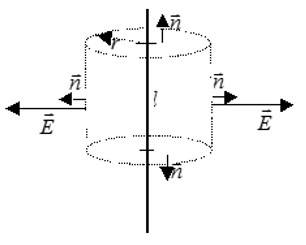
Напряженность будем искать при помощи теоремы Гаусса. Наша задача – определить зависимость напряженности от расстояния от нити. В качестве поверхности выберем цилиндр с боковыми стенками, параллельными нити. Будем учитывать только поток вектора напряженности через боковую поверхность, так как поток через основания цилиндра равен нулю:
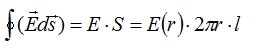
Заряд нити внутри рассматриваемой поверхности равен заряду отрезка нити длиной l:
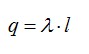
По теореме Гаусса:
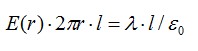
Отсюда:
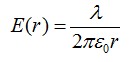
Ответ: см. выше.
Задача с применением теоремы Гаусса №4
Условие
Электрическое поле создано бесконечной заряженной прямой линией с равномерно распределённым зарядом (τ = 10 нКл/м). Определить кинетическую энергию Т2 электрона в точке 2, если в точке 1 его кинетическая энергия Т1 = 200 эВ. Расстояние точки 2 от линии равно а = 0,5 см, точки 1 – b=1,5 см.
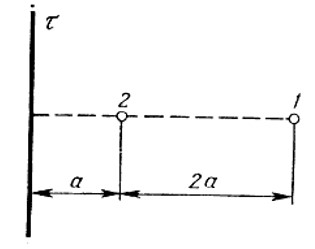
Решение
Ранее рассмотренные задачи были примерами вычисления полей с помощью теоремы Гаусса. Теперь рассмотрим задачу, которая решается сиспользованием этой информации. Из предыдущей задачи возьмем выражение для напряженности поля заряженной нити:
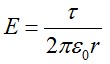
Разность потенциалов поля в двух точках будет равна:
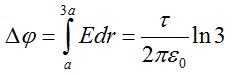
При прохождении этой разницы потенциалов электрон приобретёт кинетическую энергию:
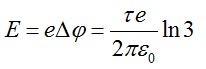
Конечная энергия частицы будет равна:
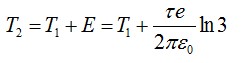
Получим:
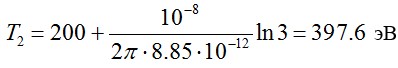
Ответ: 397.6 эВ.
Задача на теорему Гаусса №5: поток электрического поля
Условие
Два точечных заряда q и –q расположены на расстоянии 2l друг от друга. Найти поток вектора напряженности через круг радиуса R. Плоскость круга проходит через его середину и перпендикулярна отрезку прямой, соединяющей заряды.
Решение
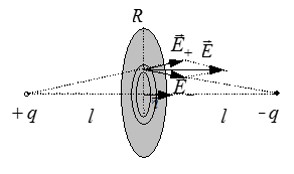
Рассмотрим элементарный поток результирующего электрического поля через бесконечно малую кольцевую зону круга:
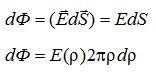
В записи потока учтено, что вектор напряженности перпендикулярен поверхности круга. Выразим напряженность электрического поля через «ро», используя подобие треугольников, показанных на рисунке:
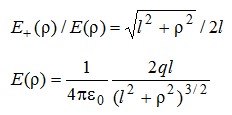
Вычисление потока сводится к взятию интеграла:
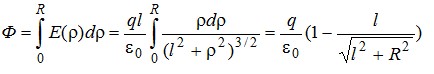
Ответ: см. выше.
Примеры применения теоремы Гаусса можно найти не только в электростатике, но и в других областях физики.
Вопросы на теорему Гаусса
Вопрос 1. Сформулируйте теорему Гаусса.
Ответ. Теорема Гаусса гласит:
Поток вектора напряженности электростатического поля через замкнутую поверхность равен алгебраической сумме зарядов внутри поверхности, деленной на эпсилон нулевое (электрическую постоянную).
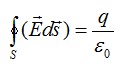
Вопрос 2. Что такое поток вектора напряженности?
Ответ. Поток вектора напряженности – скалярная физическая величина, определяемая как число линий вектора напряженности, пронизывающих некоторую поверхность S. Поток напряженности электрического поля через поверхность S конечного размера определяется как алгебраическая сумма элементарных потоков:
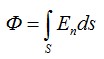
Вопрос 3. Что такое силовые линии напряженности?
Ответ. Это линии, с помощью которых используются для графического представления поля:
- касательная к силовой линии в каждой точке пространства направлена вдоль вектора поля;
- густота силовых линий пропорциональна напряженности поля в данной точке;
- поток вектора напряженности пропорционален числу силовых линий, пронизывающих поверхность.
Вопрос 4. Где начинаются и где заканчиваются силовые линии?
Ответ. Силовые линии начинаются и заканчиваются на зарядах, оставаясь непрерывными в пустом пространстве.
Вопрос 5. Верно ли утвержление: теорема Гаусса справедлива только для неподвижных зарядов.
Ответ. Нет, так как заряд частицы не зависит от ее скорости.
Нужна помощь в решении задач и других студенческих заданий? Обратитесь в профессиональный студенческий сервис за качественным решением проблем.











