Динамика – раздел механики, которому уделяется больше всего учебных часов. Уделите 5 минут на то, чтобы прочесть нашу статью и чуть больше разобраться в решении задач по динамике.
Наш телеграм – место, где мы скрупулезно отбираем, фильтруем и выкладываем все, что может быть полезно современному студенту. Под лежачий камень вода не течет, подписывайтесь!
Для начала, вопрос. Какой алгоритм решения задач по динамике? Собственно, алгоритм такой же, как и для любой задачи по физике. Мы уже писали об этом в памятке по решению задач. Не забываем держать под рукой полезные формулы, повторяем вопросы из теории, и можно приступать к практическим заданиям.
Вопросы по теме "Динамика"
Вопрос 1. Что изучает динамика?
Ответ. Динамика – раздел механики, который изучает взаимодействия между телами.
Вопрос 2. Каково основное уравнение динамики?
Ответ. Основное уравнение динамики устанавливает связь между приложенной к телу силой, его массой и ускорением тела.
Вопрос 3. Что такое вес тела и зависит ли он от местоположения тела на поверхности Земли?
Ответ. Вес – это сила, с которой тело действует на опору. Вес зависит от ускорения свободного падения, а значит и от географического местоположения на поверхности планеты. А вот масса тела всегда неизменна (за исключением движения со скоростью, близкой к скорости света).
Вопрос 4. В каких системах отсчета справедлив второй закон Ньютона?
Ответ. Второй закон Ньютона справедлив в инерциальных системах отсчета.
Вопрос 5. Сила тяжести на земле является отдельным проявлением одного из фундаментальных физических взаимодействий. Что это за взаимодействие.
Ответ. Конечно, это гравитационное взаимодействие. А сила тяжести – проявление силы всемирного тяготения.
Задачи по динамике поступательного движения с решениями
Задача №1. Определение времени движения
Условие
Тело находится у основания наклонной плоскости с углом при основании α = 30°. Коэффициент трения о поверхность равен µ = 0,6 и масса тела m = 2 кг. Сколько времени тело будет двигаться по наклонной плоскости, если его толкнуть вверх вдоль плоскости со скоростью υ0 = 20 м/с? (g = 9,8 м/с2).
Решение
Для начала, выполним рисунок:
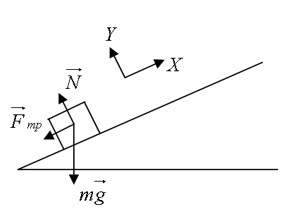
Тело будет двигаться равнозамедленно с ускорением, равным –a в течение времени t, при этом
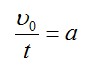
Откуда
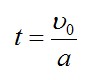
Определим ускорение a. Запишем второй закон Ньютона в векторной форме и в проекциях на оси Х и Y соответственно:
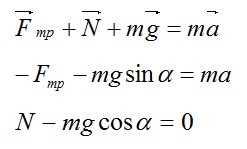
Сила трения определяется выражением
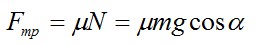
Тогда,
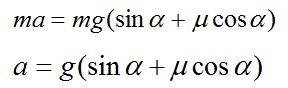
Следовательно, время, в течение которого тело будет двигаться по наклонной плоскости:
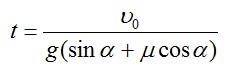
Подставим числовые значения:
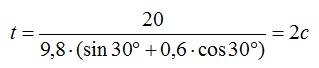
Ответ: 2 секунды.
Задача №2. Применение второго закона Ньютона
Условие
В изображенной на рисунке системе нижний брусок может двигаться по наклонной плоскости, составляющей с горизонтом угол α = 30, а верхний брусок – вдоль наклонной плоскости, составляющий с горизонтом некоторый угол β. Коэффициент трения между нижним бруском и наклонной плоскостью равен µ = 0,2, трение между верхним бруском и наклонной плоскостью отсутствует. Считая соединяющую бруски нить очень легкой и нерастяжимой, и пренебрегая массой блока и трением в его оси, найдите, при каких значениях угла β нить будет растянута.
Решение
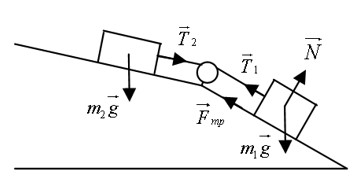
Так как тангенс угла α больше, чем коэффициент трения между бруском и поверхностью, нижний брусок будет скользить по наклонной плоскости даже при ненатянутой нити. Следовательно, в том случае, когда оба бруска движутся и нить натянута, модули ускорений брусков будут одинаковыми. Обозначим массу нижнего бруска как m1, массу верхнего бруска как m2, а силу натяжения соединяющей их нити как T. Тогда для каждого из брусков можно записать второй закон Ньютона в проекции на направление его движения:
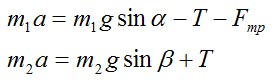
где Fтр – действующая на нижний брусок сила трения скольжения, N – действующая на него сила нормальной реакции опоры.
Так как нижний брусок не движется в направлении, перпендикулярном плоскости, то из второго закона Ньютона следует:
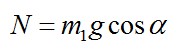
Решая совместно полученные уравнения, найдем:
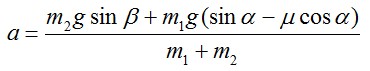
Для того, чтобы нить была натянута, должно выполняться неравенство:
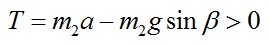
С учетом полученного выражения для модуля ускорения a, это неравенство можно переписать в следующем виде:
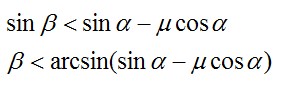
Подставим числовые значения и найдем искомый угол:
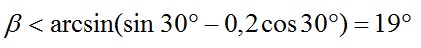
Ответ: 19°.
Задача №3. Нахождение силы
Условие
Два одинаковых груза массой M = 100 г каждый подвешены на концах невесомой и нерастяжимой нити, перекинутой через невесомый блок с неподвижной осью. На один из них кладут перегрузок массой m = 20 г, после чего система приходит в движение. Найдите модуль силы F, действующей на ось блока во время движения грузов. Трением пренебречь.
Решение
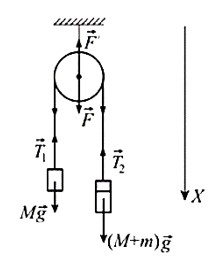
На основании второго закона Ньютона уравнение движение для обоих грузов с учетом перегрузки на одном из них в проекции на вертикальную ось, направленную вниз, выглядит следующим образом:
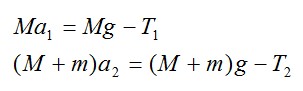
где a1 и a2 – проекции ускорений грузов M и (M+m) на вертикальную ось;
T1 и T2 – проекции сил натяжения нити на вертикальную ось. Так как нить не растяжима (по условию задачи), то
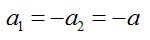
Из-за невесомости блока и нити и отсутствия трения, справедливо равенство:
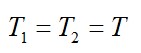
В силу третьего закона Ньютона:
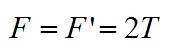
где F с индексом штрих – сила, действующая на блок со стороны его оси. Из первых двух уравнений получим:
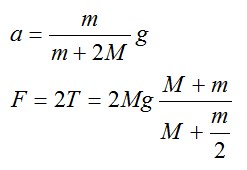
Подставим числовые значения:
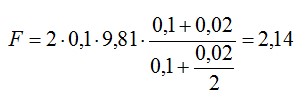
Ответ: 2,14 Ньютона.
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задачи по динамике вращательного движения с решениями
Задача №4. Нахождение числа оборотов маховика
Условие
Маховик радиусом R=0,5 м и массой 10 кг соединен с мотором при помощи приводного ремня. Натяжение ремня, идущего без скольжения, постоянно и равно Т=98 Н. Какое число оборотов в секунду будет делать маховик через Δt=10 с после начала движения. Маховик считать однородным диском.
Решение
Основное уравнение динамики вращательного движения:
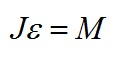
где J - момент инерции маховика. Принимая маховик за однородный диск, можно записать:
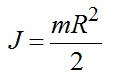
Момент силы натяжения ремня:
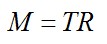
Угловое ускорение маховика:
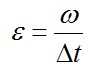
Угловая скорость маховика:
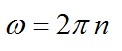
Решая уравнения, записанные выше, получим ответ:
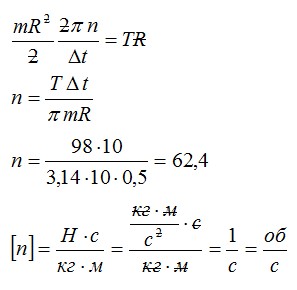
Ответ: 62,4 оборота в секунду
Задача №5. Нахождение углового ускорения
Условие
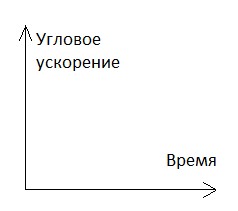
Момент силы, приложенный к вращающемуся телу изменяется по закону M=M0-αt. Момент остаётся постоянным в течение всего времени вращения. Зависимость углового ускорения от времени представлена на рисунке. Найти выражение для углового ускорения.
Решение
Согласно основному закону динамики вращательного движения:
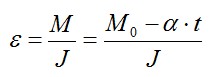
Это уравнение прямой с отрицательным углом наклона, что соответствует рисунку.
Нужна помощь в решении задач по динамике, теоретической механике, деталям машин, химии, etc? Обращайтесь за ней в профессиональный студенческий сервис.











