Как понимать относительность движения? Еще Галилей задумался над этим вопросом в 16 веке и дал на него ответ. Кстати, если вам нужно вспомнить основные понятия из кинематики, то вот отдельный материал на эту тему.
Больше ответов и актуальных студенческих вопросов – на нашем телеграм-канале.
Относительность движения: объяснение, примеры
Конечно, Галилей был не первым, кто размышлял на эту тему. Вот, что думал об относительности движения другой великий ум эпохи Возрождения – Джордано Бруно:
Как это заметили древние и современные истинные наблюдатели природы, и как это показывает тысячью способами чувственный опыт, мы можем заметить движение только посредством известного сравнения и сопоставления с каким-либо неподвижным телом. Так, люди, находящиеся в середине моря на плывущем корабле, если они не знают, что вода течёт, и не видят берегов, не заметят движения корабля. Ввиду этого можно сомневаться относительно покоя и неподвижности Земли. Я могу считать, что если бы я находился на Солнце, Луне или на других звёздах, то мне всегда казалось бы, что я нахожусь в центре неподвижного мира, вокруг которого вращается всё окружающее, вокруг которого вращается этот окружающий меня мир, в центре которого я нахожусь.
Суть относительности движения: в зависимости от выбора системы и тела отсчета, одно и то же движение может иметь разный характер и описываться по-разному.
Геоцентрическая и гелиоцентрическая системы отсчета за тело отсчета принимают соответственно землю и солнце.
Вот пример относительности механического движения. Представим, что автобус движется по дороге. По отношению к пешеходу, который стоит на остановке, его скорость равна, скажем, 60 км/ч. А относительно водителя, который едет по встречной полосе со скоростью 100 км/ч, автобус движется иначе. Говоря точнее, автобус приближается к водителю встречной машины со скоростью 160 км/ч.
При этом действует принцип относительности Галилея:
Если в двух замкнутых лабораториях, одна из которых равномерно прямолинейно (и поступательно) движется относительно другой, провести одинаковый механический эксперимент, результат будет одинаковым.
Принцип относительности по Галилею является частным случаем принципа относительности Эйнштейна.
В нашем справочнике вы более полную теорию по теме «Относительность движения». Но не будем углубляться в теорию, ведь наша сегодняшняя цель – это разбор практических задач.
Кстати! Для всех наших читателей действует скидка 10% на любой вид работы.
Задачи на относительность движения
Задача 1
Летящий звездолет посылает вперед радиосигналы длительностью t1. Внезапно он начинает принимать сигналы отраженные от находящегося впереди препятствия, длительность которых t2. С какой скоростью приближается звездолет к препятствию, если скорость распространения радиосигналов равна c?
Решение
Скорость распространения радиосигналов относительно звездолета до отражения:
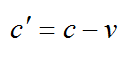
Скорость распространения радиосигналов относительно звездолета после отражения:
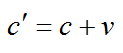
До того, как достигнуть препятствия, сигнал пролетел путь:
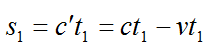
путь после отражения:
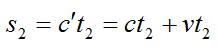
Приравняем s1 и s2 и получим:
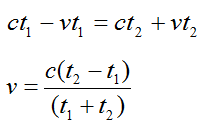
Ответ: v = c(t1 – t2)/(t1 + t2).
Задача 2
Катер проходит расстояние между двумя пунктами на реке по течению за время t1=3 часа, а против течения за t2=6 часов. Средняя скорость катера при движении туда и сразу обратно равна 10 км/ч. Найти собственную скорость катера и скорость течения реки.
Решение
По определению, средняя скорость v при равномерном прямолинейном движении равна отношению всего пройденного пути ко всему затраченному времени.
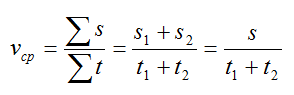
Из этого найдем расстояние между двумя пунктами:
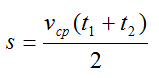
Это же расстояние можно рассчитать по формулам:
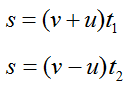
Здесь v – скорость катера, u – скорость течения. Приравняем выражения:
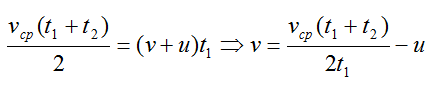
Полученное выражение для скорости катера подставим в формулу для пути:
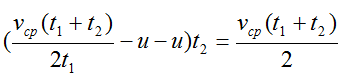
Отсюда:
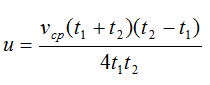
Осталось подставить данные задачи и вычислить скорость течения:
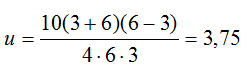
Тогда скорость катера:
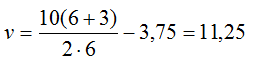
Ответ: 3,75 км/ч, 11,25 км/ч.
Задача 3
По дороге едет колонна автомобилей со скоростью 20 км/ч. Из середины колонны одновременно отправляются два мотоциклиста: один в голову колонны, другой в хвост. Первый мотоциклист приехал к месту на 6 минут раньше второго Какова длина колонны, если скорость мотоциклистов одинакова и равна 30 км/ч?
Решение
Расстояние, которое изначально нужно пройти мотоциклистам:
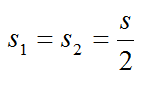
Скорость, с которой первый мотоциклист приближается к голове колоны:
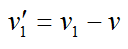
Скорость с которой второй мотоциклист приближается к хвосту колоны
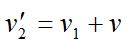
По условию:
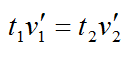
или
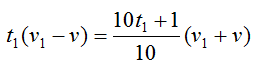
Отсюда находим время движения:
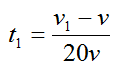
Тогда длина колонны:
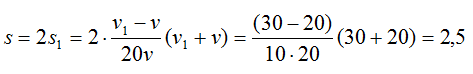
Ответ: 2,5 км.
Нужна помощь в решении задач? Профессиональный студенческий сервис всегда к вашим услугам.











